Sommenzoekers met tafels 3-4-6.
Sommenzoekers met tafels 3-4-6 apart om te oefenen. Deze Sommenzoekers met tafels 3-4-6 is de tweede in de reeks Sommenzoekers
Lees verder
puzzels
Rekenpuzzel – kruispuzzels – sommen en tafels.
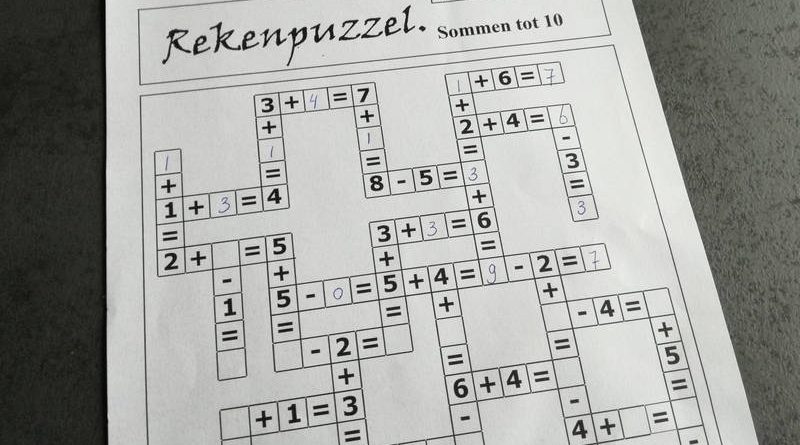
Met een rekenpuzzel – kruispuzzel breng je rekenen weer net even anders. Goed rekenen betekend meters maken. Oefenen, oefenen en
Lees verder
Coöperatieve werkvorm 13: Puzzels
De volgende coöperatieve werkvorm in deze serie is Puzzels. Deze lijkt erg op de legpuzzel, maar verschilt wel. Bij deze
Lees verder